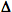 H
is a state function which means one only needs to know the
initial and final states to calculate a change in enthalpy; it does
not matter how the change occurs.
H
is a state function which means one only needs to know the
initial and final states to calculate a change in enthalpy; it does
not matter how the change occurs.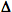 H
is a state function which means one only needs to know the
initial and final states to calculate a change in enthalpy; it does
not matter how the change occurs.
H
is a state function which means one only needs to know the
initial and final states to calculate a change in enthalpy; it does
not matter how the change occurs.
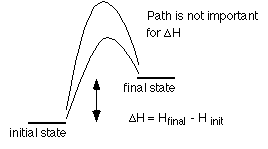
Heating water is an example of process that is path independent. Let's say in lab two students have to heat a sample of water from 23 °C to 60 °C.
The heat transfered to the water is
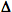 T
TSince the process is at constant pressure, and only PV work is being done, q is qp. Thus,
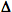 H = n s
H = n s 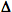 T
T
|
One student carefully heats 20 g of water from 23 °C to 60°C. Determine the 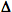 H = n s H = n s 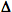 T T
|
|
Another student puts 20 g of water over a microburner and goes outside for (insert bad habit here)... The sample of water went from 23 °C to 75 °C. Before the student can continue with the experiment the sample of water must be cooled to 60 °C. Determine the To heat the water from 23 to 75 °C the amount of heat that when in is 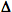 H = n s H = n s 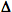 T T
But the water had to cool back to 60 °C, and while the water was cooling heat was released. 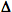 H = n s H = n s 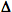 T T
So,
|
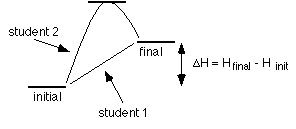
The energy that was actually transfered to the water is determined by comparing the initial and final states. Student 2 transfered extra energy into the water, but it was released by the water to the surroundings when it cooled; so, in the end, students 1 and 2 transfered the same amount of energy to the water.
What we have just demonstrated, by example, is Hess's Law.
Hess's Law holds for 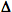 H of any
process.
H of any
process.
Typically, chemists use Hess's Law to determine 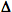 H
for reaction for a variety of reasons; the experiment may be
difficult, dangerous, or impossible, or we may be making a survey to
determine which reactions release the amount of heat we want.
H
for reaction for a variety of reasons; the experiment may be
difficult, dangerous, or impossible, or we may be making a survey to
determine which reactions release the amount of heat we want.