14C is generated in the atmosphere when a high energy neutron collides with a nitrogen nucleus. The neutron is produced when cosmic rays strike other atoms in the upper atmosphere.
14C decomposes via ß- particle emission. That is, a neutron releases a ß- particle, an electron, and becomes a proton.
The present concentration of 14C in systems interacting with the atmosphere is 1 14C atom in 7.54 x 1011 12C atoms (1.33 x 10-10% 14C in a sample of carbon). Once the living object stops interacting, living, the amount of 14C present begins to decrease. The amount of 14C cannot be directly measured because is is present in such a small amount, but the radiation emitted from the 14C nuclei can be measured.
A 1 g sample of carbon collected from the present day environment emits 1 ß- particle every 4 seconds; that is, the activity of 14C in a present day carbon sample is 0.255 Bq/g (baquerel per gram, a baquerel is one radioactive decay event per second). The age of an object can be determined by measuring the activity of the sample in question. Since, radioactive decay is a first order process-the rate of decay does not depend on the concentration of the radioactive nuclei-the rate of decay is constant. Therefore, it is simple to determine the age of the sample.
The half life of 14C is 5730 yrs; so, the rate constant k is 1.120 x 10-4 yr-1
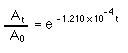
At is the activity of the sample now, A0 is the activity of the sample originally, when it was still alive. "t" is the amount of time it took for the radioactivity to fall to At. The assumption is that a living thing contains the same amount of 14C regardless of when it lived. If the previous assumption is true then A0 is also the radioactivity of a sample collected today. Therefore, "t" is the age of the sample.
Of course, the production of 14C has not been constant, but other dating methods have helped to determine how the 14C concentration has changed with time.