The ideal gas Law
Where does this come from?
Robert Boyle found
That is, the product of the pressure of a gas times the volume of a gas is a constant for a given sample of gas. In Boyle's experiments the Temperature (T) did not change, nor did the number of moles (n) of gas present. So Boyle found
but did not explore the effect the temperature, or the number of moles would have on pressure and volume.
Jaques Charles found
That is, the volume of a given sample of gas increases linearly with the temperature if the pressure (P) and the amount of the gas (n) is kept constant. So Charles found
Avagadro's Postulate
At the same temperature and pressure equal volumes of all gasses contain the same number of molecules.
V = n (RT/P)
Guy Lussac found that 1 volume of Cl2 combined with 1 volume of H2 to make 2 volumes of HCl. The equation for the reaction is
With this example we can clearly see the relationship between the number of moles of a gas, and the volume of a gas.
At constant temperature and pressure the volume of a gas is directly proportional to the number of moles of gas.
Not so coincidentally if V is constant instead of P then
At constant temperature and volume the pressure of a gas is directly proportional to the number of moles of gas.
You could remember all the different gas laws,
Or you could think about the problem a bit and use PV=nRT.
N2O is placed in a piston. Initially the volume of the piston is 3.0 L, and the pressure of the gas is 5.0 atm. The piston is used to compress the gas to a volume of 1.5 L; determine the pressure of the N2O.
well, before the compression
or
after expansion
![]()
since n, R, and T do not change
substituting
P = 1.0 x 10 L
See, if you forget all those different relationships you can just use PV=nRT.
A PV = nRT problem
What is the volume of 1 mole of an ideal gas at STP (Standard Temperature and Pressure = 0 °C, 1 atm)?
(1) V = 1(0.08206)(273.15)
V = 22.41 L
So, the volume of an ideal gas is 22.41 L/mol at STP.
This, 22.4 L, is probably the most remembered and least useful number in chemistry.
What is the volume of 5.0 g NH3 at 25 °C and 1 atm. of pressure?
Well we just found that the volume of 1 mole of an ideal gas is 22.41 L so we can use this as a conversion factor...right?
Everyone remembers that 1 mol of an ideal gas occupies a volume of 22.4 L, but this is probably the least useful number in chemistry. Alot of people forget that this relationship is only true at STP (0 °C and 1 atm.).
So, use
To use PV=nRT we need to have moles of NH3.
It is not practical to use PV=nRT as a conversion in a factor label problem so we will just solve for V.
V = 7.18 = 7.2 L NH3
Seltzer water is made by dissolving CO2 in water. Seltzer can be made at home using small containers of pressurized CO2. If one of the cartridges contains 20.00 mL CO2 at 55.00 atm at 23.0 °C and it expands into an empty seltzer bottle with a volume of 1.000 L and the resulting pressure is 1.000 atm what is the temperature of the gas.
Before the gas expands...
and
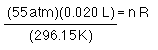
after the gas expands...
or
since R has not changed (it is called the universal gas CONSTANT for a reason) and we have not changed the number of moles of CO2...
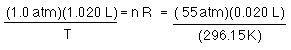
or...
What will the pressure be when the gas warms to 23.0 °C?
before expansion and warming...after expansion and warming to room temp
once again R and n have not changed, and now not even T has not changed so...
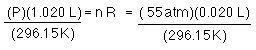
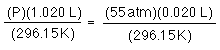
solve for P